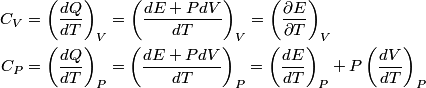 For an ideal gas, 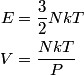 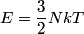 implies that implies that 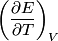 and and 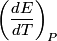 are both equal to are both equal to 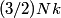 . . 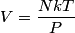 implies that implies that 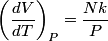 So, 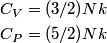 Now, let 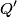 be the heat required to produce the temperature change be the heat required to produce the temperature change 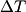 under conditions of constant pressure. Then, under conditions of constant pressure. Then,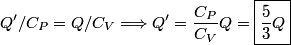 Therefore, answer (C) is correct. |
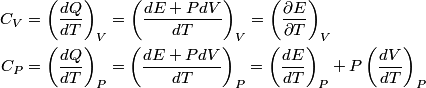 For an ideal gas, 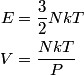 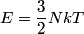 implies that implies that 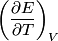 and and 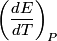 are both equal to are both equal to 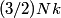 . . 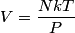 implies that implies that 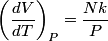 So, 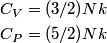 Now, let 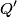 be the heat required to produce the temperature change be the heat required to produce the temperature change 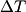 under conditions of constant pressure. Then, under conditions of constant pressure. Then,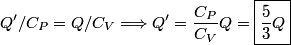 Therefore, answer (C) is correct. |